11 1/6 As A Decimal

Numeral organisation with ten as its base of operations

The decimal numeral organization (too called the base of operations-ten positional numeral system and denary ^[one] or decanary) is the standard arrangement for denoting integer and non-integer numbers. It is the extension to not-integer numbers of the Hindu–Standard arabic numeral organisation.^[2] The way of denoting numbers in the decimal system is often referred to as decimal notation.^[3]

A decimal numeral (also often simply decimal or, less correctly, decimal number), refers generally to the notation of a number in the decimal numeral system. Decimals may sometimes be identified by a decimal separator (usually "." or "," as in 25.9703 or 3,1415).^[4] Decimal may also refer specifically to the digits after the decimal separator, such as in "3.14 is the approximation of π to two decimals". Zero-digits afterwards a decimal separator serve the purpose of signifying the precision of a value.

The numbers that may exist represented in the decimal system are the decimal fractions. That is, fractions of the form a/10 ⁿ , where a is an integer, and n is a non-negative integer.

The decimal arrangement has been extended to infinite decimals for representing any existent number, by using an infinite sequence of digits subsequently the decimal separator (see decimal representation). In this context, the decimal numerals with a finite number of non-null digits after the decimal separator are sometimes chosen terminating decimals. A repeating decimal is an infinite decimal that, later on some place, repeats indefinitely the aforementioned sequence of digits (eastward.g., five.123144144144144... = five.123144 ).^[5] An infinite decimal represents a rational number, the quotient of two integers, if and but if it is a repeating decimal or has a finite number of non-goose egg digits.

Origin [edit]

X digits on two hands, the possible origin of decimal counting

Many numeral systems of aboriginal civilizations use 10 and its powers for representing numbers, peradventure because there are x fingers on two hands and people started counting past using their fingers. Examples are firstly the Egyptian numerals, so the Brahmi numerals, Greek numerals, Hebrew numerals, Roman numerals, and Chinese numerals. Very large numbers were hard to represent in these former numeral systems, and only the all-time mathematicians were able to multiply or separate big numbers. These difficulties were completely solved with the introduction of the Hindu–Arabic numeral system for representing integers. This organisation has been extended to represent some non-integer numbers, called decimal fractions or decimal numbers, for forming the decimal numeral arrangement.

Decimal notation [edit]

For writing numbers, the decimal arrangement uses ten decimal digits, a decimal mark, and, for negative numbers, a minus sign "−". The decimal digits are 0, 1, 2, iii, 4, 5, half dozen, 7, 8, 9;^[6] the decimal separator is the dot "." in many countries (mostly English-speaking),^[7] and a comma "," in other countries.^[four]

For representing a non-negative number, a decimal numeral consists of

• either a (finite) sequence of digits (such as "2017"), where the entire sequence represents an integer,

  ${\displaystyle a_{grand}a_{m-1}\ldots a_{0}}$

• or a decimal mark separating two sequences of digits (such as "20.70828")

${\displaystyle a_{m}a_{m-ane}\ldots a_{0}.b_{1}b_{2}\ldots b_{n}}$ .

If one thousand > 0, that is, if the first sequence contains at least two digits, it is generally assumed that the first digit a _m is not zero. In some circumstances it may be useful to have one or more 0's on the left; this does not change the value represented by the decimal: for case, 3.14 = 03.14 = 003.14. Similarly, if the concluding digit on the correct of the decimal mark is zero—that is, if b _northward = 0—it may be removed; conversely, trailing zeros may exist added after the decimal marking without changing the represented number; ^{[note ane]} for example, 15 = xv.0 = 15.00 and five.2 = 5.20 = 5.200.

For representing a negative number, a minus sign is placed before a _thousand .

The numeral ${\displaystyle a_{m}a_{thou-1}\ldots a_{0}.b_{1}b_{two}\ldots b_{n}}$ represents the number

${\displaystyle a_{m}10^{grand}+a_{yard-1}10^{chiliad-1}+\cdots +a_{0}10^{0}+{\frac {b_{1}}{ten^{1}}}+{\frac {b_{two}}{10^{2}}}+\cdots +{\frac {b_{due north}}{x^{north}}}}$ .

The integer part or integral part of a decimal numeral is the integer written to the left of the decimal separator (see also truncation). For a not-negative decimal numeral, it is the largest integer that is not greater than the decimal. The part from the decimal separator to the right is the fractional office, which equals the divergence between the numeral and its integer function.

When the integral part of a numeral is cypher, it may occur, typically in computing, that the integer part is not written (for example, .1234, instead of 0.1234). In normal writing, this is mostly avoided, considering of the gamble of confusion between the decimal mark and other punctuation.

In brief, the contribution of each digit to the value of a number depends on its position in the numeral. That is, the decimal organisation is a positional numeral system.

Decimal fractions [edit]

Decimal fractions (sometimes called decimal numbers, especially in contexts involving explicit fractions) are the rational numbers that may be expressed as a fraction whose denominator is a power of x.^[8] For instance, the decimals ${\displaystyle 0.8,14.89,0.00024,i.618,3.14159}$ stand for the fractions 8 / 10 , 1489 / 100 , 24 / 100000 , + 1618 / 1000 and + 314159 / 100000 , and are therefore decimal numbers.

More than generally, a decimal with n digits after the separator (a point or comma) represents the fraction with denominator 10 ⁿ , whose numerator is the integer obtained by removing the separator.

It follows that a number is a decimal fraction if and but if it has a finite decimal representation.

Expressed as a fully reduced fraction, the decimal numbers are those whose denominator is a product of a power of ii and a power of 5. Thus the smallest denominators of decimal numbers are

${\displaystyle 1=2^{0}\cdot 5^{0},2=2^{i}\cdot v^{0},4=2^{two}\cdot 5^{0},5=two^{0}\cdot 5^{1},viii=2^{iii}\cdot 5^{0},10=2^{one}\cdot 5^{i},16=2^{four}\cdot v^{0},20=2^{ii}\cdot five^{i},25=2^{0}\cdot 5^{2},\ldots }$

Real number approximation [edit]

Decimal numerals do not let an exact representation for all real numbers, due east.thou. for the existent number π. Withal, they permit approximating every real number with whatsoever desired accuracy, east.g., the decimal 3.14159 approximates the real π, beingness less than 10^−five off; so decimals are widely used in science, applied science and everyday life.

More precisely, for every real number x and every positive integer n, there are two decimals L and u with at most northward digits after the decimal mark such that L ≤ x ≤ u and (u − L) = x⁻ⁿ .

Numbers are very often obtained equally the result of measurement. As measurements are subject to measurement doubt with a known upper leap, the result of a measurement is well-represented by a decimal with north digits afterward the decimal mark, as soon every bit the absolute measurement fault is bounded from in a higher place by 10^−north . In practice, measurement results are often given with a certain number of digits later on the decimal point, which indicate the error bounds. For instance, although 0.080 and 0.08 denote the same number, the decimal numeral 0.080 suggests a measurement with an fault less than 0.001, while the numeral 0.08 indicates an absolute error bounded past 0.01. In both cases, the truthful value of the measured quantity could be, for example, 0.0803 or 0.0796 (see also pregnant figures).

Space decimal expansion [edit]

For a real number x and an integer due north ≥ 0, let [10] _n denote the (finite) decimal expansion of the greatest number that is non greater than ten that has exactly n digits after the decimal marker. Let d _i announce the terminal digit of [ten] _i . It is straightforward to see that [10] _n may be obtained by appending d _{due north} to the right of [x] _n−ane . This style one has

[x] _n = [x]₀.d ₁ d ₂...d _{due north−ane} d _n ,

and the difference of [ten] _{northward−1} and [ten] _northward amounts to

${\displaystyle \left\vert \left[x\correct]_{n}-\left[x\right]_{northward-1}\correct\vert =d_{n}\cdot 10^{-n}<10^{-north+ane}}$ ,

which is either 0, if d _north = 0, or gets arbitrarily small as due north tends to infinity. Co-ordinate to the definition of a limit, ten is the limit of [x] _n when northward tends to infinity. This is written as ${\textstyle \;x=\lim _{n\rightarrow \infty }[x]_{n}\;}$ or

x = [x]₀.d ₁ d _two...d _{due north} ...,

which is chosen an space decimal expansion of ten .

Conversely, for any integer [x]₀ and any sequence of digits ${\textstyle \;(d_{north})_{northward=1}^{\infty }}$ the (infinite) expression [ten]₀.d ₁ d ₂...d _north ... is an infinite decimal expansion of a real number x . This expansion is unique if neither all d _northward are equal to ix nor all d _n are equal to 0 for n large enough (for all due north greater than some natural number Due north).

If all d _n for due north > N equal to 9 and [x] _n = [x]₀.d ₁ d _two...d _n , the limit of the sequence ${\textstyle \;([ten]_{n})_{northward=1}^{\infty }}$ is the decimal fraction obtained past replacing the final digit that is not a 9, i.e.: d _N , past d _N + 1, and replacing all subsequent 9s by 0s (see 0.999...).

Whatsoever such decimal fraction, i.e.: d _n = 0 for n > N , may exist converted to its equivalent space decimal expansion by replacing d _N past d _N − 1 and replacing all subsequent 0s by 9s (run across 0.999...).

In summary, every existent number that is not a decimal fraction has a unique space decimal expansion. Each decimal fraction has exactly two infinite decimal expansions, i containing only 0s after some place, which is obtained by the above definition of [x] _n , and the other containing but 9s after some place, which is obtained by defining [10] _n equally the greatest number that is less than x, having exactly north digits after the decimal mark.

Rational numbers [edit]

Long division allows computing the space decimal expansion of a rational number. If the rational number is a decimal fraction, the division stops eventually, producing a decimal numeral, which may be prolongated into an infinite expansion past adding infinitely many zeros. If the rational number is non a decimal fraction, the division may continue indefinitely. Yet, equally all successive remainders are less than the divisor, there are only a finite number of possible remainders, and later some place, the same sequence of digits must be repeated indefinitely in the quotient. That is, 1 has a repeating decimal. For instance,

1 / 81 = 0.012345679012... (with the grouping 012345679 indefinitely repeating).

The antipodal is besides true: if, at some point in the decimal representation of a number, the aforementioned string of digits starts repeating indefinitely, the number is rational.

For case, if x is	0.4156156156...
then 10,000ten is	4156.156156156...
and 10x is	4.156156156...
so 10,000x − 10x, i.e. 9,990x, is	4152.000000000...
and 10 is	4152 / 9990

or, dividing both numerator and denominator by half dozen, 692 / 1665 .

Decimal computation [edit]

Most modern computer hardware and software systems commonly use a binary representation internally (although many early on computers, such as the ENIAC or the IBM 650, used decimal representation internally).^[nine] For external use by computer specialists, this binary representation is sometimes presented in the related octal or hexadecimal systems.

For almost purposes, withal, binary values are converted to or from the equivalent decimal values for presentation to or input from humans; reckoner programs express literals in decimal past default. (123.1, for example, is written as such in a reckoner program, even though many figurer languages are unable to encode that number precisely.)

Both calculator hardware and software also use internal representations which are finer decimal for storing decimal values and doing arithmetic. Oft this arithmetic is done on data which are encoded using some variant of binary-coded decimal,^{[10] [11]} especially in database implementations, only at that place are other decimal representations in utilize (including decimal floating point such equally in newer revisions of the IEEE 754 Standard for Floating-Point Arithmetics).^[12]

Decimal arithmetic is used in computers so that decimal fractional results of calculation (or subtracting) values with a fixed length of their fractional part e'er are computed to this same length of precision. This is especially important for fiscal calculations, e.g., requiring in their results integer multiples of the smallest currency unit of measurement for book keeping purposes. This is not possible in binary, because the negative powers of ${\displaystyle 10}$ accept no finite binary fractional representation; and is more often than not impossible for multiplication (or division).^{[thirteen] [14]} Come across Arbitrary-precision arithmetics for exact calculations.

History [edit]

The world'south primeval decimal multiplication tabular array was made from bamboo slips, dating from 305 BCE, during the Warring States period in China.

Many ancient cultures calculated with numerals based on ten, sometimes argued due to human hands typically having x fingers/digits.^[fifteen] Standardized weights used in the Indus Valley civilisation (c.  3300–1300 BCE) were based on the ratios: 1/xx, 1/10, i/v, ane/ii, 1, 2, v, 10, 20, 50, 100, 200, and 500, while their standardized ruler – the Mohenjo-daro ruler – was divided into 10 equal parts.^{[16] [17] [18]} Egyptian hieroglyphs, in bear witness since effectually 3000 BCE, used a purely decimal organization,^[19] as did the Cretan hieroglyphs (c.  1625−1500 BCE) of the Minoans whose numerals are closely based on the Egyptian model.^{[20] [21]} The decimal arrangement was handed down to the consecutive Bronze Age cultures of Greece, including Linear A (c. 18th century BCE−1450 BCE) and Linear B (c. 1375−1200 BCE) – the number organization of classical Hellenic republic as well used powers of ten, including, Roman numerals, an intermediate base of v.^[22] Notably, the polymath Archimedes (c. 287–212 BCE) invented a decimal positional system in his Sand Reckoner which was based on 10^{8 [22]} and after led the German mathematician Carl Friedrich Gauss to lament what heights science would have already reached in his days if Archimedes had fully realized the potential of his ingenious discovery.^[23] Hittite hieroglyphs (since 15th century BCE) were also strictly decimal.^[24]

Some not-mathematical ancient texts such as the Vedas, dating back to 1700–900 BCE brand employ of decimals and mathematical decimal fractions.^[25]

The Egyptian hieratic numerals, the Greek alphabet numerals, the Hebrew alphabet numerals, the Roman numerals, the Chinese numerals and early Indian Brahmi numerals are all not-positional decimal systems, and required big numbers of symbols. For instance, Egyptian numerals used different symbols for ten, 20 to 90, 100, 200 to 900, thousand, 2000, 3000, 4000, to x,000.^[26] The world's earliest positional decimal system was the Chinese rod calculus.^[27]

The earth's primeval positional decimal system
Upper row vertical course
Lower row horizontal form

History of decimal fractions [edit]

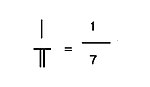
counting rod decimal fraction i/7

Decimal fractions were showtime developed and used by the Chinese in the finish of 4th century BCE,^[28] and then spread to the Eye East and from there to Europe.^{[27] [29]} The written Chinese decimal fractions were non-positional.^[29] However, counting rod fractions were positional.^[27]

Qin Jiushao in his volume Mathematical Treatise in Ix Sections (1247^[30]) denoted 0.96644 by

寸

, meaning

寸

096644

J. Lennart Berggren notes that positional decimal fractions appear for the kickoff time in a book by the Arab mathematician Abu'l-Hasan al-Uqlidisi written in the 10th century.^[31] The Jewish mathematician Immanuel Bonfils used decimal fractions around 1350, anticipating Simon Stevin, but did not develop any notation to stand for them.^[32] The Farsi mathematician Jamshīd al-Kāshī claimed to take discovered decimal fractions himself in the 15th century.^[31] Al Khwarizmi introduced fraction to Islamic countries in the early 9th century; a Chinese author has alleged that his fraction presentation was an exact re-create of traditional Chinese mathematical fraction from Sunzi Suanjing.^[27] This grade of fraction with numerator on top and denominator at lesser without a horizontal bar was also used past al-Uqlidisi and by al-Kāshī in his piece of work "Arithmetic Key".^{[27] [33]}

A forerunner of modern European decimal annotation was introduced past Simon Stevin in the 16th century.^[34]

John Napier introduced using the period (.) to carve up the integer part of a decimal number from the fractional part in his volume on constructing tables of logarithms, published posthumously in 1620.^{[35] : p. 8, archive p. 32)}

Natural languages [edit]

A method of expressing every possible natural number using a gear up of 10 symbols emerged in India. Several Indian languages show a straightforward decimal arrangement. Many Indo-Aryan and Dravidian languages have numbers between 10 and 20 expressed in a regular pattern of addition to 10.^[36]

The Hungarian linguistic communication also uses a straightforward decimal system. All numbers between x and 20 are formed regularly (e.chiliad. 11 is expressed as "tizenegy" literally "one on ten"), as with those betwixt twenty and 100 (23 as "huszonhárom" = "three on twenty").

A straightforward decimal rank organization with a word for each order (10 十 , 100 百 , thousand 千 , x,000 万 ), and in which 11 is expressed every bit ten-one and 23 equally two-x-three, and 89,345 is expressed as viii (ten thousands) 万 9 (chiliad) 千 iii (hundred) 百 4 (tens) 十 5 is found in Chinese, and in Vietnamese with a few irregularities. Japanese, Korean, and Thai accept imported the Chinese decimal arrangement. Many other languages with a decimal system have special words for the numbers between 10 and xx, and decades. For example, in English 11 is "eleven" not "ten-one" or "one-teen".

Incan languages such as Quechua and Aymara take an almost straightforward decimal organization, in which 11 is expressed every bit x with one and 23 as two-ten with three.

Some psychologists suggest irregularities of the English names of numerals may hinder children'due south counting ability.^[37]

Other bases [edit]

Some cultures practise, or did, use other bases of numbers.

• Pre-Columbian Mesoamerican cultures such as the Maya used a base-20 arrangement (perhaps based on using all 20 fingers and toes).
• The Yuki linguistic communication in California and the Pamean languages^[38] in Mexico have octal (base-viii) systems because the speakers count using the spaces between their fingers rather than the fingers themselves.^[39]
• The existence of a non-decimal base in the primeval traces of the Germanic languages is attested by the presence of words and glosses meaning that the count is in decimal (cognates to "ten-count" or "tenty-wise"); such would be expected if normal counting is not decimal, and unusual if it were.^{[40] [41]} Where this counting system is known, information technology is based on the "long hundred" = 120, and a "long thousand" of 1200. The descriptions like "long" merely appear later the "small hundred" of 100 appeared with the Christians. Gordon's Introduction to Former Norse p. 293, gives number names that vest to this system. An expression cognate to 'one hundred and eighty' translates to 200, and the cognate to 'ii hundred' translates to 240. Goodare details the use of the long hundred in Scotland in the Center Ages, giving examples such as calculations where the carry implies i C (i.e. one hundred) as 120, etc. That the general population were non alarmed to encounter such numbers suggests common plenty use. Information technology is as well possible to avoid hundred-similar numbers by using intermediate units, such equally stones and pounds, rather than a long count of pounds. Goodare gives examples of numbers similar vii score, where one avoids the hundred by using extended scores. At that place is besides a newspaper past W.H. Stevenson, on 'Long Hundred and its uses in England'.^{[42] [43]}
• Many or all of the Chumashan languages originally used a base-iv counting organization, in which the names for numbers were structured according to multiples of 4 and 16.^[44]
• Many languages^[45] utilise quinary (base-5) number systems, including Gumatj, Nunggubuyu,^[46] Kuurn Kopan Noot^[47] and Saraveca. Of these, Gumatj is the merely true 5–25 linguistic communication known, in which 25 is the higher group of 5.
• Some Nigerians use duodecimal systems.^[48] And so did some small communities in India and Nepal, as indicated past their languages.^[49]
• The Huli language of Papua New Guinea is reported to have base of operations-15 numbers.^[l] Ngui means xv, ngui ki means fifteen × 2 = 30, and ngui ngui means fifteen × xv = 225.
• Umbu-Ungu, besides known equally Kakoli, is reported to have base of operations-24 numbers.^[51] Tokapu means 24, tokapu talu means 24 × two = 48, and tokapu tokapu means 24 × 24 = 576.
• Ngiti is reported to accept a base-32 number organization with base of operations-4 cycles.^[45]
• The Ndom language of Papua New Guinea is reported to take base-6 numerals.^[52] Mer means half-dozen, mer an thef ways 6 × 2 = 12, nif ways 36, and nif thef means 36×2 = 72.

Run into also [edit]

• Algorism
• Binary-coded decimal (BCD)
• Decimal classification
• Decimal computer
• Decimal fourth dimension
• Decimal representation
• Decimal section numbering
• Decimal separator
• Decimalisation
• Densely packed decimal (DPD)
• Duodecimal
• Octal
• Scientific annotation
• Serial decimal
• SI prefix

Notes [edit]

1. ^ Sometimes, the extra zeros are used for indicating the accurateness of a measurement. For example, "fifteen.00 1000" may betoken that the measurement error is less than one centimetre (0.01 yard), while "fifteen m" may mean that the length is roughly fifteen metres and that the mistake may exceed 10 centimetres.

References [edit]

1. ^ "denary". Oxford English Dictionary (Online ed.). Oxford University Printing. (Subscription or participating institution membership required.)
2. ^ Cajori, Florian (Feb 1926). "The History of Arithmetic. Louis Charles Karpinski". Isis. University of Chicago Press. viii (ane): 231–232. doi:ten.1086/358384. ISSN 0021-1753.
3. ^ Yong, Lam Lay; Se, Ang Tian (Apr 2004). Fleeting Footsteps. World Scientific. 268. doi:10.1142/5425. ISBN978-981-238-696-0 . Retrieved March 17, 2022.
4. ^ ^{a b} Weisstein, Eric Westward. (March x, 2022). "Decimal Point". Wolfram MathWorld . Retrieved March 17, 2022. {{cite web}}: CS1 maint: url-status (link)
5. ^ The vinculum (overline) in v.123144 indicates that the '144' sequence repeats indefinitely, i.e. five.123144 144 144 144....
6. ^ In some countries, such every bit Arab speaking ones, other glyphs are used for the digits
7. ^ Weisstein, Eric Due west. "Decimal". mathworld.wolfram.com . Retrieved 2020-08-22 .
8. ^ "Decimal Fraction". Encyclopedia of Mathematics . Retrieved 2013-06-18 .
9. ^ "Fingers or Fists? (The Choice of Decimal or Binary Representation)", Werner Buchholz, Communications of the ACM, Vol. 2 #12, pp. 3–xi, ACM Press, December 1959.
10. ^ Schmid, Hermann (1983) [1974]. Decimal Ciphering (i (reprint) ed.). Malabar, Florida: Robert E. Krieger Publishing Company. ISBN0-89874-318-4.
11. ^ Schmid, Hermann (1974). Decimal Ciphering (1st ed.). Binghamton, New York: John Wiley & Sons. ISBN0-471-76180-10.
12. ^ Decimal Floating-Indicate: Algorism for Computers, Cowlishaw, Mike F., Proceedings 16th IEEE Symposium on Calculator Arithmetics, ISBN 0-7695-1894-X, pp. 104–11, IEEE Comp. Soc., 2003
13. ^ Decimal Arithmetic – FAQ
14. ^ Decimal Floating-Point: Algorism for Computers, Cowlishaw, One thousand. F., Proceedings 16th IEEE Symposium on Computer Arithmetics (ARITH sixteen), ISBN 0-7695-1894-X, pp. 104–11, IEEE Comp. Soc., June 2003
15. ^ Dantzig, Tobias (1954), Number / The Language of Science (4th ed.), The Gratuitous Press (Macmillan Publishing Co.), p. 12, ISBN0-02-906990-iv
16. ^ Sergent, Bernard (1997), Genèse de l'Inde (in French), Paris: Payot, p. 113, ISBN ii-228-89116-9
17. ^ Coppa, A.; et al. (2006). "Early Neolithic tradition of dentistry: Flintstone tips were surprisingly effective for drilling molar enamel in a prehistoric population". Nature. 440 (7085): 755–56. Bibcode:2006Natur.440..755C. doi:ten.1038/440755a. PMID 16598247. S2CID 6787162.
18. ^ Bisht, R. Southward. (1982), "Excavations at Banawali: 1974–77", in Possehl, Gregory L. (ed.), Harappan Civilisation: A Gimmicky Perspective, New Delhi: Oxford and IBH Publishing Co., pp. 113–24
19. ^ Georges Ifrah: From One to Zero. A Universal History of Numbers, Penguin Books, 1988, ISBN 0-xiv-009919-0, pp. 200–xiii (Egyptian Numerals)
20. ^ Graham Flegg: Numbers: their history and meaning, Courier Dover Publications, 2002, ISBN 978-0-486-42165-0, p. 50
21. ^ Georges Ifrah: From 1 to Cypher. A Universal History of Numbers, Penguin Books, 1988, ISBN 0-14-009919-0, pp. 213–18 (Cretan numerals)
22. ^ ^{a b} "Greek numbers". Retrieved 2019-07-21 .
23. ^ Menninger, Karl: Zahlwort und Ziffer. Eine Kulturgeschichte der Zahl, Vandenhoeck und Ruprecht, third. ed., 1979, ISBN 3-525-40725-4, pp. 150–53
24. ^ Georges Ifrah: From 1 to Zero. A Universal History of Numbers, Penguin Books, 1988, ISBN 0-14-009919-0, pp. 218f. (The Hittite hieroglyphic arrangement)
25. ^ (Atharva Veda v.15, ane–11)
26. ^ Lam Lay Yong et al. The Fleeting Footsteps pp. 137–39
27. ^ ^{a b c d e} Lam Lay Yong, "The Evolution of Hindu–Arabic and Traditional Chinese Arithmetic", Chinese Science, 1996 p. 38, Kurt Vogel notation
28. ^ "Ancient bamboo slips for calculation enter globe records volume". The Institute of Archaeology, Chinese Academy of Social Sciences . Retrieved x May 2017.
29. ^ ^{a b} Joseph Needham (1959). "Decimal System". Science and Civilisation in Mainland china, Book III, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Printing.
30. ^ Jean-Claude Martzloff, A History of Chinese Mathematics, Springer 1997 ISBN iii-540-33782-2
31. ^ ^{a b} Berggren, J. Lennart (2007). "Mathematics in Medieval Islam". In Katz, Victor J. (ed.). The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. p. 530. ISBN978-0-691-11485-9.
32. ^ Gandz, Southward.: The invention of the decimal fractions and the awarding of the exponential calculus by Immanuel Bonfils of Tarascon (c. 1350), Isis 25 (1936), 16–45.
33. ^ Lay Yong, Lam. "A Chinese Genesis, Rewriting the history of our numeral organization". Archive for History of Exact Sciences. 38: 101–08.
34. ^ B. L. van der Waerden (1985). A History of Algebra. From Khwarizmi to Emmy Noether. Berlin: Springer-Verlag.
35. ^ Napier, John (1889) [1620]. The Construction of the Wonderful Catechism of Logarithms. Translated by Macdonald, William Rae. Edinburgh: Blackwood & Sons – via Internet Archive. In numbers distinguished thus by a menstruation in their midst, whatever is written later the menstruum is a fraction, the denominator of which is unity with as many cyphers after information technology every bit there are figures later the period.
36. ^ "Indian numerals". Ancient Indian mathematics. Archived from the original on 2007-09-29. Retrieved 2015-05-22 .
37. ^ Azar, Beth (1999). "English words may hinder math skills development". American Psychological Association Monitor. 30 (4). Archived from the original on 2007-x-21.
38. ^ Avelino, Heriberto (2006). "The typology of Pame number systems and the limits of Mesoamerica as a linguistic expanse" (PDF). Linguistic Typology. 10 (i): 41–lx. doi:10.1515/LINGTY.2006.002. S2CID 20412558.
39. ^ Marcia Ascher. "Ethnomathematics: A Multicultural View of Mathematical Ideas". The College Mathematics Periodical. JSTOR 2686959.
40. ^ McClean, R. J. (July 1958), "Observations on the Germanic numerals", High german Life and Messages, 11 (4): 293–99, doi:10.1111/j.1468-0483.1958.tb00018.x, Some of the Germanic languages appear to show traces of an ancient blending of the decimal with the vigesimal organisation .
41. ^ Voyles, Joseph (October 1987), "The cardinal numerals in pre-and proto-Germanic", The Journal of English language and Germanic Philology, 86 (four): 487–95, JSTOR 27709904 .
42. ^ Stevenson, W.H. (1890). "The Long Hundred and its uses in England". Archaeological Review. December 1889: 313–22.
43. ^ Poole, Reginald Lane (2006). The Exchequer in the twelfth century : the Ford lectures delivered in the Academy of Oxford in Michaelmas term, 1911. Clark, NJ: Lawbook Substitution. ISBNane-58477-658-seven. OCLC 76960942.
44. ^ At that place is a surviving listing of Ventureño language number words up to 32 written down by a Spanish priest ca. 1819. "Chumashan Numerals" by Madison S. Beeler, in Native American Mathematics, edited past Michael P. Closs (1986), ISBN 0-292-75531-seven.
45. ^ ^{a b} Hammarström, Harald (17 May 2007). "Rarities in Numeral Systems". In Wohlgemuth, January; Cysouw, Michael (eds.). Rethinking Universals: How rarities bear on linguistic theory (PDF). Empirical Approaches to Language Typology. Vol. 45. Berlin: Mouton de Gruyter (published 2010). Archived from the original (PDF) on nineteen August 2007.
46. ^ Harris, John (1982). Hargrave, Susanne (ed.). "Facts and fallacies of aboriginal number systems" (PDF). Work Papers of SIL-AAB Series B. 8: 153–81. Archived from the original (PDF) on 2007-08-31.
47. ^ Dawson, J. "Australian Aborigines: The Languages and Customs of Several Tribes of Aborigines in the Western District of Victoria (1881), p. xcviii.
48. ^ Matsushita, Shuji (1998). Decimal vs. Duodecimal: An interaction between ii systems of numeration. 2nd Meeting of the AFLANG, October 1998, Tokyo. Archived from the original on 2008-ten-05. Retrieved 2011-05-29 .
49. ^ Mazaudon, Martine (2002). "Les principes de construction du nombre dans les langues tibéto-birmanes". In François, Jacques (ed.). La Pluralité (PDF). Leuven: Peeters. pp. 91–119. ISBNninety-429-1295-ii.
50. ^ Cheetham, Brian (1978). "Counting and Number in Huli". Papua New Guinea Periodical of Teaching. 14: xvi–35. Archived from the original on 2007-09-28.
51. ^ Bowers, Nancy; Lepi, Pundia (1975). "Kaugel Valley systems of reckoning" (PDF). Journal of the Polynesian Society. 84 (3): 309–24. Archived from the original (PDF) on 2011-06-04.
52. ^ Owens, Kay (2001), "The Work of Glendon Lean on the Counting Systems of Papua New Guinea and Oceania", Mathematics Didactics Research Journal, 13 (1): 47–71, Bibcode:2001MEdRJ..13...47O, doi:10.1007/BF03217098, S2CID 161535519, archived from the original on 2015-09-26

11 1/6 As A Decimal,

Source: https://en.wikipedia.org/wiki/Decimal

Posted by: wardposs1950.blogspot.com

Share this post